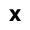La mecánica del caracol
Ciencia
Los quipus: las matemáticas incas y el experimento de la aguja de Buffon
Los incas utilizaban cuerdas anudadas para representar información numérica. El BCBL busca voluntarios para un experimento sobre Alzheimer y bilingüismo. Agujas y probabilidad para sacar el número Pi.
-
 52:29 min
52:29 min



Se dice que la escritura nació por necesidad contable: contar mercancías, animales, que se compraban y vendían, o se almacenaban o transportaban. Así, las primeras marcas tenían un significado numéricos del que poco a poco acabaría derivando, el alfabeto y la escritura, el reflejo del habla oral. Las formas utilizadas por las antiguas culturas para crear sus libros de contabilidad son variadas, y una de las más peculiares es la que desarrollaron los incas. Los quipus son cuerdas anudadas con las que los incas representaban su escritura numérica y registraban la información que les interesaba. Las matemáticas de la cultura inca es el tema que abordamos con Raúl Ibáñez.
El Basque Center on Cognition, Brain and Language (BCBL) de San Sebastián prepara un ambicioso estudio para demostrar que el bilingüismo puede retrasar varios años la aparición del alzhéimer. El objetivo de esta investigación es comprobar si el dominio de dos idiomas refuerza los mecanismos de compensación que ayudan a un cerebro enfermo a funcionar correctamente más tiempo, según ha informado el BCBL en un comunicado. Para llevar a cabo el experimento, el centro donostiarra busca 120 voluntarios de entre 65 y 80 años, repartidos entre monolingües y bilingües.
Las personas interesadas en participar en la investigación pueden escribir un correo electrónico a participa@bcbl.eu o ponerse en contacto con el centro en el teléfono 943 309 300.
Manu Hernández dedica su sección de experimentos a la aguja de Buffon, un clásico problema de probabilidad matemática planteado por el matemático y naturalista Georges Lous Leclerc, conde de Buffon en 1773. Si se multiplica por 2 el número de alfileres que se dejan caer sobre un papel marcado con rayas de la longitud de un alfiler, y se divide por el número de alfileres que cortan alguna de esas rayas, se obtendrá un valor aproximado al número Pi.